Deze tabel toont de frequentie t.o.v. de toonhoogte op gitaar en andere instrumenten, gebaseerd op de standaard tuning A4=440 Hz
Laten we eerst een paar wiskunde oefeningen doen 🙂 !
In de gelijkzwevende stemming is de toonafstand tussen naastliggende tonen voor alle tonen even groot.
Daarom is deze verhouding gelijk aan de twaalfde-machtswortel van 2: MACHT(2;1/12) = 1.05946309.
Zo is van A5 met een toonhoogte van 880 Hz, de daarboven liggende A# dus ongeveer 932,3 Hz (= 1,05946309 × 880).
Bijvoorbeeld, als formule in Microsoft Excel
A#4 is 1 semitone hoger dan A4
A#4 = 440*MACHT(MACHT(2;1/12);1) = 466.1 Hz
B4 is 2 semitones hoger dan A4
B4 = 440*MACHT(MACHT(2;1/12);2) = 493.8 Hz
A5 is 12 semitones hoger dan A4
B4 = 440*MACHT(MACHT(2;1/12);12) = 880 Hz
| noot | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| C | 16,35 | 32,7 | 65,4 | 130,8 | 261,6 | 523,2 | 1046 | 2093 | 4186 | 8372 |
| C# | 17,32 | 34,64 | 69,29 | 138,5 | 277,1 | 554,3 | 1108 | 2217 | 4434 | 8869 |
| D | 18,35 | 36,7 | 73,41 | 146,8 | 293,6 | 587,3 | 1174 | 2349 | 4698 | 9397 |
| D# | 19,44 | 38,89 | 77,78 | 155,5 | 311,1 | 622,2 | 1244 | 2489 | 4978 | 9956 |
| E | 20,6 | 41,2 | 82,4 | 164,8 | 329,6 | 659,2 | 1318 | 2637 | 5274 | 10548 |
| F | 21,82 | 43,65 | 87,3 | 174,6 | 349,2 | 698,4 | 1396 | 2793 | 5587 | 11175 |
| F# | 23,12 | 46,24 | 92,49 | 184,9 | 369,9 | 739,9 | 1479 | 2959 | 5919 | 11839 |
| G | 24,49 | 48,99 | 97,99 | 195,9 | 391,9 | 783,9 | 1567 | 3135 | 6271 | 12543 |
| G# | 25,95 | 51,91 | 103,8 | 207,6 | 415,3 | 830,6 | 1661 | 3322 | 6644 | 13289 |
| A | 27,5 | 55 | 110 | 220 | 440 | 880 | 1760 | 3520 | 7040 | 14080 |
| A# | 29,13 | 58,27 | 116,5 | 233 | 466,1 | 932,3 | 1864 | 3729 | 7458 | 14917 |
| B | 30,86 | 61,73 | 123,4 | 246,9 | 493,8 | 987,7 | 1975 | 3951 | 7902 | 15804 |
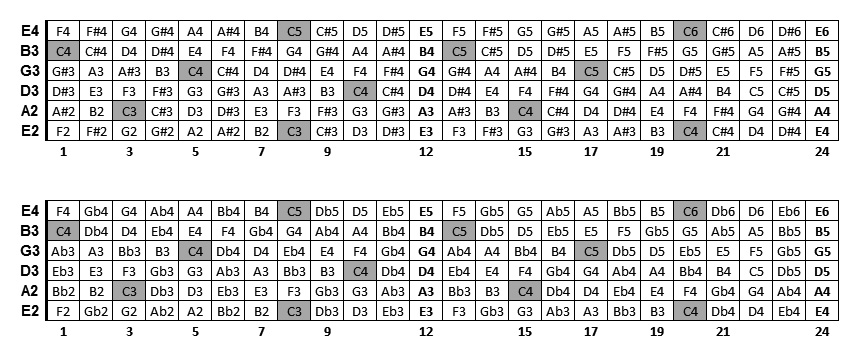
Noten op gitaar fretboard (met kruisen # en mollen b)
Opmerking : een C# en Db is in praktijk in onze westerse muziek dezelfde noot (enharmonische). Let wel, muziektheoretisch gezien is een C# niet hetzelfde als een Db !