PITCH AND FREQUENCY OF NOTES IN 440Hz standard tuning
This table shows the frequency compared to the pitch on guitar and other instruments, based on the standard tuning in our modern western music system with A4=440 Hz
🔒 This is a members-only zone.
Join our Guitar Studio family today to unlock exclusive benefits and become part of our musicians’ community!
Let’s do some math exercises first! In the equally floating tuning, the tone distance between adjacent tones is the same for all tones. Therefore, this ratio is equal to the twelfth square root of power of 2: POWER(2;1/12) = 1.05946309. This means if we take A5 with a frequency pitch of 880 Hz, the semitone above A# is approximately 932,3 Hz (= 1,05946309 × 880).
Example with the formula in Microsoft Excel
A#4 is 1 semitone higher than A4
A#4 = 440*POWER(POWER(2;1/12);1) = 466.1 Hz
B4 is 2 semitones higher than A4
B4 = 440*POWER(POWER(2;1/12);2) = 493.8 Hz
A5 is 12 semitones higher than A4
B4 = 440*POWER(POWER(2;1/12);12) = 880 Hz
Table of Diatonic Scales (table)
All scales in a clear table, scale degrees with corresponding triad and seventh chords. Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, Locrian. Sharps and flats to quickly identify the key of a score through key signature. Circle of fourths and fifths with keys, major and relative minor scales.
| NOTE | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| C | 16,35 | 32,7 | 65,4 | 130,8 | 261,6 | 523,2 | 1046 | 2093 | 4186 | 8372 |
| C# / Db | 17,32 | 34,64 | 69,29 | 138,5 | 277,1 | 554,3 | 1108 | 2217 | 4434 | 8869 |
| D | 18,35 | 36,7 | 73,41 | 146,8 | 293,6 | 587,3 | 1174 | 2349 | 4698 | 9397 |
| D# / Eb | 19,44 | 38,89 | 77,78 | 155,5 | 311,1 | 622,2 | 1244 | 2489 | 4978 | 9956 |
| E | 20,6 | 41,2 | 82,4 | 164,8 | 329,6 | 659,2 | 1318 | 2637 | 5274 | 10548 |
| F | 21,82 | 43,65 | 87,3 | 174,6 | 349,2 | 698,4 | 1396 | 2793 | 5587 | 11175 |
| F# / Gb | 23,12 | 46,24 | 92,49 | 184,9 | 369,9 | 739,9 | 1479 | 2959 | 5919 | 11839 |
| G | 24,49 | 48,99 | 97,99 | 195,9 | 391,9 | 783,9 | 1567 | 3135 | 6271 | 12543 |
| G# / Ab | 25,95 | 51,91 | 103,8 | 207,6 | 415,3 | 830,6 | 1661 | 3322 | 6644 | 13289 |
| A | 27,5 | 55 | 110 | 220 | 440 | 880 | 1760 | 3520 | 7040 | 14080 |
| A# / Bb | 29,13 | 58,27 | 116,5 | 233 | 466,1 | 932,3 | 1864 | 3729 | 7458 | 14917 |
| B | 30,86 | 61,73 | 123,4 | 246,9 | 493,8 | 987,7 | 1975 | 3951 | 7902 | 15804 |
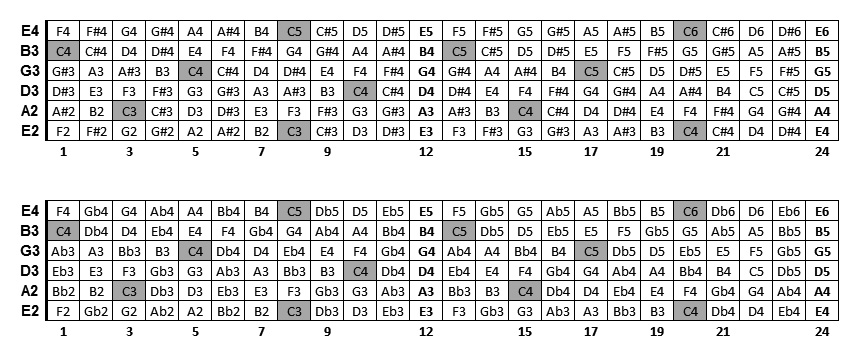
Notes on the guitar fretboard (with sharps # and flats b)
Note: a C# and Db is in our Western music exact the same note (enharmonic).
BUT, in music theory a C# is not the same as a Db!
Notes on the guitar and bass fretboard + frequencies (Hz)
Note: the frequency (Hz) values are rounded without decimals for space-saving purposes.
